

오늘 소개할 문제는 LeetCode 40번 문제 "Combination Sum II"입니다. 이 문제는 전형적인 백트래킹 문제라고 판단해서 실수할 수 있는 문제입니다. 백트래킹 알고리즘에서 어떤 부분을 주의해야 할지, 최적화는 어떻게 하면 좋은지에 대한 실마리를 포함하고 있는 문제입니다. 아래의 한 유저가 말씀해주신 것 처럼, 대부분의 회사의 채용 코딩인터뷰 문제 목록에 포함되어 있는 문제이기도 합니다.


문제 설명
리트코드 40번 Combination Sum II 문제에서는 중복된 숫자가 포함된 배열에서 합이 특정 목표값(target)이 되는 모든 고유한 조합을 찾아야 합니다. 주어진 배열의 각 숫자는 한 번만 사용할 수 있으며, 같은 조합이 중복되어 결과에 포함되지 않도록 해야 합니다.
문제 해결 과정
1. 초기 접근 : 문제 이해하기
이렇게 조합을 구하는 문제는 백트래킹을 사용하여 해결할 수 있습니다. 그러나, 주의할 점은 입력 배열 'candidates' 에 중복된 숫자가 있을 수 있다는 것입니다. 따라서, 중복된 조합이 생성되지 않도록 신경 써야 합니다.
2-1. 기본적인 백트래킹 로직
1. 입력 배열을 오름차순으로 정렬합니다. 이는 중복된 조합을 피하기 위해 필요합니다.
2. 백트래킹 함수를 정의합니다.
- 현재 인덱스, 현재 조합을 인자로 받습니다.
- 현재 조합의 합계가 'target'과 같으면 결과 리스트에 추가합니다.
- 현재 조합의 합계가 'target'보다 크면 더 이상 탐색하지 않습니다.
- 그 외의 경우, 현재 인덱스부터 시작하여 반복문을 돌며, 다음 숫자를 선택합니다.
- 선택한 숫자를 현재 조합에 추가하고 answer에 없는 조합이라면, 재귀 호출을 합니다.
처음에 시도한 코드는 아래과 같습니다. (시간 초과 이슈-TLE)
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates = sorted(candidates)
if sum(candidates) < target:
return []
def backtracking(idx, curr):
if sum(curr) == target:
answer.append(curr)
return
if sum(curr) > target:
return
for i in range(idx, len(candidates)):
if curr + [candidates[i]] not in answer:
backtracking(i + 1, curr + [candidates[i]])
answer = []
backtracking(0, [])
return answer
이 코드에서는 시간초과가 발생했습니다. 시간초과가 발생하는 이유는 2가지로 바라볼 수 있습니다.
1) 중복된 계산(반복적인 합계 계산)
: `sum(curr)` 를 재귀호출마다 계산하는 것은 리스트의 길이가 길어질수록 많은 시간을 소모합니다. 리스트의 모든 요소를 더하는 작업이 반복되므로, 성능이 저하되는 것입니다.
2) 비효율적인 중복 체크
: `if curr + [candidates[i]] not in answer` 과 같은 부분에서 중복을 체크하는 방식은 비효율적입니다. 리스트를 계속해서 합쳐서 중복 여부를 체크하는 데 시간이 많이 소요되기 때문입니다.
2-2. 최적화 방법(개선 사항)
1) 현재 합계 추적 변수 사용(`curr_sum`인자 도입)
: `sum(curr)` 대신, `curr_sum`변수를 사용하여 현재까지의 합계를 추적하면, 매번 리스트 전체를 합산하지 않아도 됩니다.
2) 중복 조합 방지 로직 추가
: 정렬된 배열에서 같은 숫자가 연속으로 등장하는 경우, 이전에 선택한 동일한 숫자를 건너뛰어 중복된 조합 생성을 방지합니다. 즉, 중복된 숫자를 건너뛰기 위해 현재 숫자가 이전 숫자와 동일한 경우를 체크합니다.
3) 리스트 상태 복원
: `curr.append(candidates[i])`로 리스트에 요소를 추가하고, 백트래킹 후에는 `curr.pop()`으로 상태를 복원합니다. 이렇게 함으로써, 불필요한 복사 없이 리스트를 효율적으로 관리할 수 있습니다. 즉, 재귀 호출 후에는 선택한 숫자를 현재 조합에서 제거하여 상태를 복원합니다.
개선된 코드는 아래와 같습니다.
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates = sorted(candidates)
answer = []
def backtracking(idx, curr, curr_sum):
if curr_sum == target:
answer.append(curr[:])
return
if curr_sum > target:
return
for i in range(idx, len(candidates)):
# 중복된 숫자 건너뛰기
if i > idx and candidates[i] == candidates[i-1]:
continue
curr.append(candidates[i])
# 현재 숫자를 선택하여 재귀 호출
backtracking(i + 1, curr, curr_sum + candidates[i])
curr.pop()
backtracking(0, [], 0)
return answer
candidates[i] == candidates[i-1] 를 체크 해야 하는 것이 어떤 의미이고 무슨 역할을 하는지 모르겠는데요?
`candidates[i] == candidates[i-1]` 과 같이 같은 숫자가 연속으로 등장하는지 체크하는 것은 예시를 통해 설명해보겠습니다.
주어진 candidates 리스트에서는 같은 숫자가 여러 번 등장할 수 있습니다. 만약 이런 숫자들을 조합할 때, 모두 사용하게 되면, 동일한 결과를 여러 번 구하게 될 수 있습니다.
예를 들어, `[1,1,2]` 라는 리스트가 주어졌을 때, 2개의 1이 있으므로, `[1,2]` 라는 조합이 중복되어 생성될 수 있다는 말입니다.
이처럼, 오름차순으로 정렬된 리스트에서 중복된 숫자가 연속으로 나오는 경우, 앞에서 이미 그 숫자를 사용한 경우라면, 다시 그 숫자를 사용하지 않도록 하여 중복된 조합을 생성하지 않도록 해야 합니다. 그래서, for 문 안쪽에 아래와 같은 코드를 추가해야 합니다.
if i > idx and candidates[i] == candidates[i-1]: # 중복 제거
continue
코드를 분석해보자면, 아래와 같습니다
- `i > idx` 는 현재 인덱스 `i`가 백트래킹의 시작 인덱스 `idx`보다 커야 한다는 것을 의미합니다. 이는 첫 번째 요소는 비교하지 않고 넘어가겠다는 의미입니다.
- `candidates[i] == candidates[i-1]` 조건은 현재 숫자 `candidates[i]`가 바로 이전 숫자 `candidates[i-1]`와 동일한지를 확인하고, 만약 같다면, 이전에 이미 이 숫자를 사용한 경우이므로, 동일한 조합을 다시 사용하지 않도록 `continue`로 반복문의 다음 단계로 넘어갑니다.
2-3. 추가 설명 및 주의할 점
1. `curr.append(candidates[i])`와 `curr.pop()`의 의미
: 코드에서 `curr.append(candidates[i])`는 현재 조합 리스트에 새로운 숫자를 추가하는 동작입니다. 이 때, 리스트가 원본 그대로 유지되도록 하기 위해 백트래킹이 끝난 후에 `curr.pop()`을 통해 마지막에 추가한 요소를 제거하여 리스트의 상태를 복원합니다.
append 하고 다시 pop 하는 작업과 answer에 curr 의 복사본을 넣어야 하는 것이 귀찮다면, 아래와 같은 방법처럼 curr 에 직접적으로 [candidates[i]]를 더함으로써 인자로 전해줘도 됩니다. 이렇게 하는 작업도, curr 에 candidates[i] 원소를 더해서 새로운 리스트를 전해주는 방식과 동일합니다.
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
answer = []
def backtracking(idx, curr, curr_sum):
if curr_sum == target:
answer.append(curr)
return
if curr_sum > target:
return
for i in range(idx, len(candidates)):
# 중복된 숫자 건너뛰기
if i > idx and candidates[i] == candidates[i - 1]:
continue
# 현재 숫자를 선택하여 재귀 호출
backtracking(i + 1, curr + [candidates[i]], curr_sum + candidates[i])
backtracking(0, [], 0)
return answer
2. `answer.append(curr[:])`와 얕은 복사
`answer.append(curr[:])`는 `curr`리스트의 현재 상태를 복사하여 결과 리스트에 추가하는 작업입니다. 이 때, `[:]`를 사용하여 얕은복사를 수행하는 이유는, `curr`리스트가 백트래킹 과정에서 계속 변하기 때문에 복사본을 사용하여 나중에 `curr`이 변경되더라도, 이미 추가된 결과에 영향을 미치지 않도록 하기 위함입니다.
3. `curr_sum 인자와 sum(curr)`의 차이
`curr_sum` 인자는 현재 조합의 합을 추적하는 데 사용됩니다. `sum(curr)`를 반복해서 계산하는 것은 리스트의 크기가 커질수록 성능이 저하될 수 있기 때문에, 각 단계에서 합을 업데이트하며 추적하는 방식이 훨씬 효율적입니다.
3. 최종 코드 및 결과
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates = sorted(candidates)
answer = []
def backtracking(idx, curr, curr_sum):
if curr_sum == target:
answer.append(curr[:])
return
if curr_sum > target:
return
for i in range(idx, len(candidates)):
# 중복된 숫자 건너뛰기
if i > idx and candidates[i] == candidates[i-1]:
continue
curr.append(candidates[i])
# 현재 숫자를 선택하여 재귀 호출
backtracking(i + 1, curr, curr_sum + candidates[i])
curr.pop()
backtracking(0, [], 0)
return answer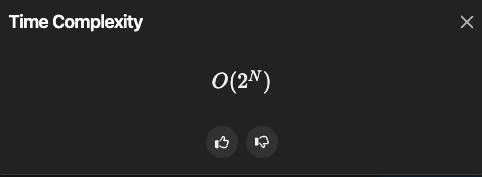
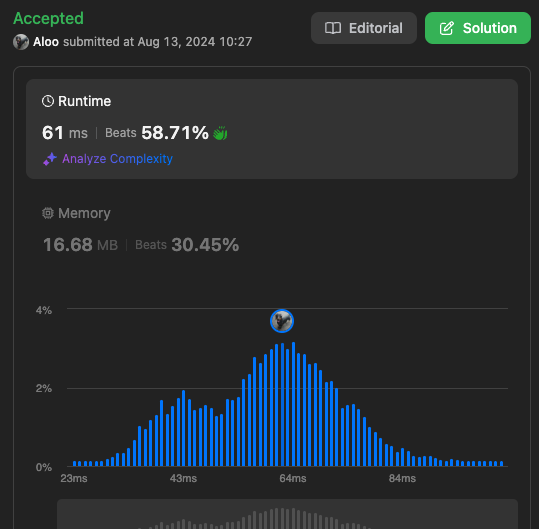
Lessons Learned
이상으로 40. Combination Sum II 문제에 대해 정리해봤습니다. 이 포스팅에서는 리트코드 40번 문제를 해결하기 위한 최적화된 접근법을 다루었습니다. 백트래킹과 중복 제거 로직을 통해 성능을 크게 향상시킬 수 있었으며, 리스트의 복사 및 상태 복원에 대한 개념도 살펴보았습니다.
'컴퓨터 공부 > 📚 Leetcode' 카테고리의 다른 글
| [리트코드/leetcode/python] 1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance (0) | 2024.07.26 |
|---|---|
| [리트코드/leetcode/python] 912. Sort an Array (0) | 2024.07.25 |
| [리트코드/leetcode/python] 2392. Build a Matrix With Conditions (0) | 2024.07.21 |
| [리트코드/leetcode/python] 560. Subarray Sum Equals K (0) | 2024.01.28 |
| [리트코드/leetcode/python] 380. Insert Delete GetRandom O(1) (0) | 2024.01.16 |
