오늘은 누적합과 관련한 SubArray의 수를 구하는 문제를 가져와봤습니다. 문제는 짧지만 구현하기는 쉽지 않습니다.
문제 이해부터 해보겠습니다.
주어진 정수 배열 'nums'와 정수 'k'가 있을 때, 합이 'k'와 같은 연속된 부분 배열의 개수를 찾는 것이 이 문제의 목표입니다.
예를 들어, num = [1,2,-1,3] 이고 , k = 2 인 경우에는 두 개의 부분 배열 [1,2,-1] 과 [2] 가 목표 합을 만족합니다. 즉 답은 2가 됩니다.
이 문제를 봤을 때 뭔가 누적합을 이용한 풀이를 생각할 수 있습니다. 하지만, 제한 조건을 봤을 때 시간복잡도도 고려해야 문제를 통과할 수 있을 것 같습니다. 또, 주어진 배열에서 연속된 부분 배열 중 합이 k인 경우의 수를 찾는 것이 핵심인데, 여기서 배열에 음수가 포함될 수 있기 때문에, 부분 배열의 합이 비선형적으로 변할 수 있습니다.
일반적으로 연속된 부분 배열 문제에서는 '슬라이딩 윈도우' 기법이 사용됩니다. 하지만, 음수의 존재로 인해 이 방법은 이 문제를 푸는 데에는 적합하지 않습니다.
실제로 Discussion을 보면, 한 유저가 왜 '슬라이딩 윈도우' 알고리즘으로 풀면 안되냐는 질문했습니다.

그에 대한 댓글로 아래와 같은 설명이 있었습니다.

댓글에 대해 설명해보자면, 해당 유저가 제시해주신 예제는 nums = [1,2,-1,3] 이고, k = 2 입니다. 이 경우에, 슬라이딩 윈도우 방식을 사용하면, 처음에 left와 right 가 모두 0이 되고, sum은 nums[0] 즉 1이 됩니다.
다음 단계에서, left <= right 조건을 만족하기 때문에, right를 1 증가시키는데, 이 부분 배열은 [1,2] 가 되고 합은 3이 될 것입니다.
하지만, k 가 2기 때문에, 두 가지 선택지가 있습니다.
1. right 를 1 증가시켜 다음 부분 배열을 [1,2,-1] 로 만듭니다.
2. left 를 1 증가시켜 다음 부분 배열을 [2] 로 만듭니다.
이 두 가지 선택지는 모두 다음 합이 2가 될 수 있습니다. 왜냐하면, 배열에 음수가 포함되어 있어서, right 포인터를 앞으로 이동시킬 때 합계가 항상 증가하지 않기 때문입니다.
만약 첫 번째 옵션을 선택한다면, 두 번째 옵션에서 나올 수 있는 유효한 부분 배열 하나를 놓칠 수 있습니다. 왜냐하면 right 를 이전 인덱스로 돌릴 수 없기 때문입니다.
반대로 두 번째 옵션을 선택한다면, 첫 번째 옵션에서 나올 수 있는 유효한 부분 배열 하나를 놓칠 수 있습니다. 왜냐하면 left를 이전 인덱스로 돌릴 수 없기 때문입니다.
따라서, 이 문제는 슬라이딩 윈도우 방식보다는 누적 합과 해시맵을 사용하는 방식이 더 적합합니다. 이 방법은 음수가 포함된 배열에서도 모든 가능한 부분 배열을 고려할 수 있으며, 슬라이딩 윈도우 방식에서 발생할 수 있는 유효한 부분 배열의 누락 문제를 해결할 수 있습니다.
그렇다면, 누적 합과 해시맵을 어떻게 사용해야 할까요?
.
..
...
누적합을 사용하면, 각 인덱스에서의 총합을 효과적으로 추적할 수 있고,
해시맵을 사용하여 이 누적 합과 그것이 발생한 횟수를 기록함으로써, 우리는 특정 부분 배열의 합이 k가 되는 경우를 빠르게 식별할 수 있습니다.
.
..
...
그럼 아래와 같은 힌트를 보고 직접 구현해봅시다.
1. 누적 합 계산 : 배열을 순회하면서 각 인덱스에서의 누적 합을 계산합니다.
2. 해시맵 사용 : 해시맵을 사용하여 각 누적합의 발생 횟수를 기록합니다. 이 때, 해시맵의 키는 누적합이고, 값은 그 누적합이 발생한 횟수입니다.
3. 부분 배열 찾기 : 배열을 순회하면서, 현재 누적 합에서 k 를 뺀 값이 해시맵에 존재하는지 확인합니다. 만약 존재한다면, 그 값은 k를 합으로 하는 부분 배열의 개수에 기여하게 됩니다.
4. 예외 처리 : 누적 합이 정확이 k일 때를 처리하기 위해, 해시맵에 누적합 0이 1번 발생했다고 초기화하는 것이 중요합니다. 즉, 해시맵을 만들 때, 누적합이 0인 경우를 고려하여 '{0:1}' 로 초기화해야하는 뜻입니다. 이것은 아무것도 선택하지 않은 상태에서 합이 0이 될 수 있음을 나타냅니다.
핵심 아이디어는 현재 누적합에서 k 를 뺀 값이 이전에 해시맵에 저장된 적이 있는지 없는지를 확인하는 것입니다. 만약 저장된 적이 있다면, 그 만큼의 부분 배열이 k 와 같은 합을 가질 수 있다는 것을 의미하니까요.
예를 들어, 현재 누적합이 'currentSum' 이고, 'currentSum - k' 가 해시맵에 존재한다면, 'currentSum - ( currentSum - k ) = k' 를 만족하는 부분 배열이 존재한다는 뜻입니다.
이러한 생각을 토대로 코드를 작성하면 아래와 같이 작성할 수 있습니다.
class Solution(object):
def subarraySum(self, nums, k):
accumulation = {0:1} # 누적 합이 0인 경우를 위해 초기화
cnt = 0
currentSum = 0
for i,n in enumerate(nums):
currentSum += n # 현재 누적 합 계산
# 현재 누적 합에서 k를 뺀 값이 이전에 존재하는지 확인
if (currentSum-k) in accumulation:
cnt += accumulation[currentSum-k]
# 누적 합을 해시맵에 추가하거나 업데이트
accumulation[currentSum] = accumulation.get(currentSum,0) + 1
return cnt
해당 코드는 배열 'nums'의 각 요소를 순회합니다.
1. 현재 요소를 'currentSum'에 더하고,
2. 'currentSum - k' 가 해시맵 'accumulation'에 존재하는지 확인을 합니다. 만약 존재한다면, 그 값을 이전에도 만들 수 있었다는 의미니까 최종 카운트횟수 cnt에그 값(accumulation[currentSum-k])을 더해줍니다.
3. 'currentSum'의 발생 횟수는 순회할 때마다 'accumulation[currentSum-k]'를 업데이트합니다.
코드를 더 간결하게 하고 싶다면, 아래와 같이 작성할 수도 있습니다.
class Solution(object):
def subarraySum(self, nums, k):
accumulation = {0:1} # 누적 합이 0인 경우를 위해 초기화
cnt = 0
currentSum = 0
for i,n in enumerate(nums):
currentSum += n # 현재 누적 합 계산
# 현재 누적 합에서 k를 뺀 값이 이전에 존재하는지 확인
cnt += accumulation.get(currentSum-k, 0)
# 누적 합을 해시맵에 추가하거나 업데이트
accumulation[currentSum] = accumulation.get(currentSum,0) + 1
return cnt
해당 알고리즘의 시간복잡도는 O(n), 공간 복잡도는 O(n) 입니다.
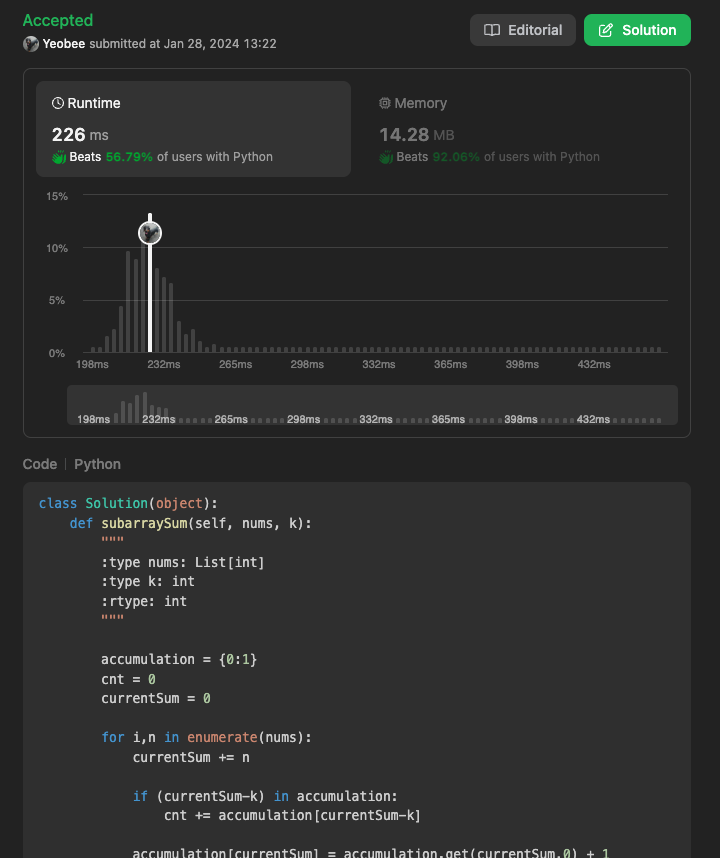
이처럼, "560. Subarray Sum Equals K" 는 동적 프로그래밍과 해시맵을 사용하여 효율적으로 해결할 수 있는 문제입니다.
연관된 문제로 325. Maximum Size Subarray Sum Equals k 가 있으니 풀어보시면 좋습니다.
'컴퓨터 공부 > 📚 Leetcode' 카테고리의 다른 글
| [리트코드/leetcode/python] 912. Sort an Array (0) | 2024.07.25 |
|---|---|
| [리트코드/leetcode/python] 2392. Build a Matrix With Conditions (0) | 2024.07.21 |
| [리트코드/leetcode/python] 380. Insert Delete GetRandom O(1) (0) | 2024.01.16 |
| [리트코드/leetcode/python] 1235. Maximum Profit in Job Scheduling (2) | 2024.01.06 |
| [리트코드/leetcode/python] 2870. Minimum Number of Operations to Make Array Empty (2) | 2024.01.04 |

