

오늘은 matrix 와 관련한 문제를 가져와봤습니다.해당 문제는 Hard 라고 표기되어 있지만, Medium 정도의 난이도로 잘 생각한다면 코드는 길어져도 풀 수 있는 문제입니다.
문제 설명
리트코드 2392번 Build a Matrix With Conditions 문제는 주어진 조건에 따라 k * k 행렬을 구성하는 문제입니다. 행과 열에 대한 조건이 주어졌을 때, 각 숫자가 주어진 순서에 맞게 매트릭스에 배치되어야 합니다.
각 조건은 '[a,b]' 형태로 주어지며, rowConditions 에서는 숫자 'a'가 숫자 'b'보다 윗 행에 위치해야 하고, colConditions 에서는 숫자 'a'가 숫자 'b'보다 왼쪽 열에 위치해야 함을 의미합니다. 나머지 행렬위치에는 0으로 채우면 됩니다. 만약 만족하는 행렬이 없다면 빈 리스트를 출력해야 합니다.
문제 해결 과정
1. 초기 접근 : 문제 이해하기
처음 이 문제를 접했을 때, 주어진 조건들을 어떻게 matrix에 반영할지 막막했습니다. Discussion에서 사람들의 접근법을 살펴봤습니다. 많은 사람들이 topological sort 에 대해 말하고 있었습니다. topological sort 는 위상정렬을 의미합니다. 행렬에서 위상정렬을 말한다는 것은 그래프에 대해 먼저 생각해봐야 할 것 같습니다.

위상 정렬은 방향 그래프의 노드들을 순서대로 나열하는 방법입니다. 이 문제에서는 주어진 조건들이 사실상 방향 그래프의 간선으로 볼 수 있습니다. 즉, 각 숫자가 주어진 순서를 만족하도록 행과 열에 배치하기 이전에 먼저 위상정렬을 통해 그래프를 구성해야 합니다.
2. 위상 정렬을 이용한 해결 방법
위상정렬을 사용하여 각 조건을 만족하는 순서를 찾아야 합니다. 이를 위해 아래와 같은 단계를 거쳐야 합니다.
1. 그래프 구성하기 : 행과 열 조건을 그래프로 표현합니다.
2. 위상 정렬 구현 : 그래프를 기반으로 위상 정렬을 수행합니다.
3. 매트릭스 구성하기 : 위상 정렬 결과를 이용해 매트릭스를 채웁니다.
그럼 먼저 행과 열의 조건에 맞는 그래프와 위상정렬 리스트를 구성해봅시다.
rowConditions 에 맞는 indegree 와 colConditions 에 맞는 indegree 를 구성해보면, 아래와 같습니다.
class Solution:
def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:
# 최종답 matrix
matrix = [[0] * k for _ in range(k)]
# 행 그래프
row_graph = [[] for _ in range(k+1)]
# 열 그래프
col_graph = [[] for _ in range(k+1)]
# 행 indegree 리스트, 열 indegree 리스트
row_indegree = [0] * (k+1)
col_indegree = [0] * (k+1)
# rowConditions a->b, b노드에는 간선이 들어오니까 + 1
for a, b in rowConditions:
row_graph[a].append(b)
row_indegree[b] += 1
# colConditions a->b, b노드에는 간선이 들어오니까 + 1
for a, b in colConditions:
col_graph[a].append(b)
col_indegree[b] += 1
rowConditions 를 기준으로 [a,b] 라고 하면 a 노드에서 b노드로 간선을 추가하고, colConditions 를 기준으로 [a,b]라고 하면 a 노드에서 b노드로의 간선을 추가하면 됩니다.
주어진 입력 예시로 보면, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]] 이므로 이를 그래프로 나타내보면, 아래 그림과 같습니다.
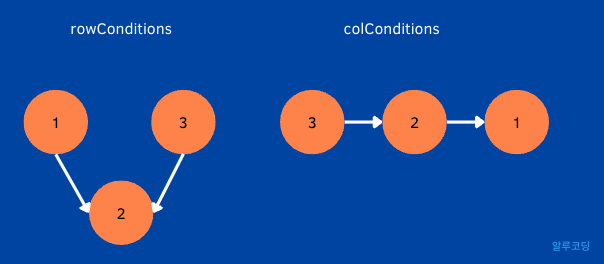
그럼 이제 이렇게 구성한 그래프를 기반으로 위상정렬을 수행하기 위해 함수를 작성해야 합니다.
위상정렬의 정형화된 함수는 큐를 사용하는 방식입니다. (위상정렬 함수에 대한 자세한 설명 참조)
from collections import deque
class Solution:
def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:
def topology_sort(graph,indegree):
res = []
q = deque()
for i in range(1,k+1):
if indegree[i] == 0:
q.append(i)
while q :
node = q.popleft()
res.append(node)
for nei in graph[node]:
indegree[nei] -= 1
if indegree[nei] == 0:
q.append(nei)
if len(res) == k:
return res
else:
# cycle or not all nodes are connected
return []
r = topology_sort(row_graph, row_indegree)
c = topology_sort(col_graph, col_indegree)
if not r or not c:
return [] # # cycle or not all nodes are connected
'topology_sort' 함수에서 큐에 원소를 넣는 부분 이후, 큐에서 원소를 하나씩 빼면서 그 원소와 연결된 모든 노드들의 indgree를 감소시키고, indgree가 0이 되는 노드를 큐에 추가하는 방식으로 정렬된 결과를 res에 담아 반환하면 됩니다.
이 때, 위상정렬 함수는 'row_graph' 와 'col_graph' 각각 수행해야 하므로, 함수 내의 행용과 열용으로 사용할 수 있도록 graph와 indgree 인자를 받아서 사용하게끔 했습니다.
res 에 담긴 원소들은 결국 k개만큼 들어가 있어야 합니다. 적거나 그것보다 많으면, 모든 노드들끼리 연결되지 않았거나 노드들간의 사이클이 형성된 그래프이기 때문에 최종적으로 행렬을 만들 수가 없습니다.
'row_graph' 와 'col_graph' 에 대해 각각 잘 res가 반환됐다면, 각 반환값을 이용해서 올바른 순서로 matrix의 올바른 위치에 배치해야 합니다. 위 코드를 기준으로 말씀드리자면, r 과 c 를 사용하여 행과 열의 인덱스를 매핑합니다. 예를 들어, r[i] 는 i 번째 행에 위치하고, c[j]는 j 번째 열에 위치하게 됩니다.
"r[i] 는 i 번째 행에 위치하고, c[j]는 j 번째 열에 위치하게 됩니다." 이 말이 어떻게 보장되는건가요?
'r' 과 'c' 를 사용하여 행과 열의 인덱스를 매핑하는 것이 어떻게 보장되는지 설명하겠습니다.
위상 정렬을 통해 구한 'r' 과 'c' 는 각각 행과 열에 대한 순서입니다. 이 순서가 유일한 이유는 다음과 같습니다.
1. 위상 정렬의 유일성
- 위상 정렬 결과는 그래프의 위상 순서를 유지합니다. 즉, 'r[i]' 는 'r[i+1]' 보다 앞서야 하는 노드이고, 마찬가지로 'c[j]'는 'c[j+1]' 보다 앞서야 하는 노드입니다. 이는 주어진 조건들('rowConditions' 와 'colConditions') 에 의해 정의됩니다.
- 만약 위상 정렬이 성공적으로 수행되면, 주어진 모든 조건을 만족하는 유일한 순서가 나옵니다.
2. Matrix 에서 위치 보장
- 'r[i]' 가 i번째 행에 위치한다는 것은 'r'의 i 번째 요소가 매트릭스의 i 번째 행에 놓인다는 것을 의미합니다.
- 같은 방식으로 'c[j]'가 j 번째 열에 위치한다는 것은 'c'의 j 번째 요소가 매트릭스의 j 번째 열에 놓인다는 것을 의미합니다.
예를 들어, 입력 예제 1번과 같은 조건을 살펴봅시다.
- rowConditions = [[1,2],[3,2]]
- colConditions = [[2,1],[3,2]]
위상정렬을 수행하면, 다음과 같은 결과가 나올 수 있습니다.
- ' r = [1, 3, 2]' (1이 3보다 앞에 있고, 3이 2보다 앞에 있어야 함)
- ' c =[3, 2, 1]' (3이 2보다 앞에 있고, 2가 1보다 앞에 있어야 함)
이 순서에 따라 매트릭스를 채우면, 다음과 같이 됩니다.
- 행의 순서 : 1번째 행 → 2번째 행 → 3번째 행
- 열의 순서 : 3번째 열 → 2번째 열 → 1번째 열
여기까지 잘 따라오셨나요? 이제 거의 다 왔습니다. 위상 정렬 결과를 사용해 매트릭스를 채우는 과정에서 매트릭스의 정확한 위치에 배치되도록 각 숫자의 행과 열 위치를 매핑하는 것이 중요합니다. 이것만 해결하면 정답 매트릭스를 얻어낼 수 있습니다.
from collections import deque
class Solution:
def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:
r = topology_sort(row_graph,row_indegree)
c = topology_sort(col_graph,col_indegree)
if not r or not c:
return []
row_pos = {num : i for i,num in enumerate(r)}
col_pos = {num : j for j,num in enumerate(c)}
for num in range(1,k+1):
matrix[row_pos[num]][col_pos[num]] = num
return matrix
해당 코드는 최종 매트릭스를 채우는 작업입니다. 'r' 과 'c' 에서 반환된 순서를 사용하여 행과 열의 인덱스를 매핑합니다. 예를 들어, 'r[i]'는 i번째 행에 위치하고, 'c[j]'는 j번째 열에 위치하게 됩니다.
말그대로, 숫자가 1부터 k 까지 있으니까 그 중에 특정 숫자(num)가 행렬의 [i,j] 에 위치한다고 이해하시면 됩니다. 그 매핑작업을 'row_pos' 와 'col_pos' 에서 한 것입니다. 그리고 key값 특정 숫자(num)의 대응되는 value값은 인덱스이므로 matrix[i][j] 에 특정숫자(num)을 배치하면 모든 작업이 마무리됩니다.
3. 최종 코드 및 결과
from collections import deque
class Solution:
def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:
matrix = [[0] * k for _ in range(k)]
row_graph = [[] for _ in range(k+1)]
col_graph = [[] for _ in range(k+1)]
row_indegree = [0] * (k+1)
col_indegree = [0] * (k+1)
for a,b in rowConditions:
row_graph[a].append(b)
row_indegree[b] += 1
for a,b in colConditions:
col_graph[a].append(b)
col_indegree[b] += 1
def topology_sort(graph,indegree):
res = []
q = deque()
for i in range(1,k+1):
if indegree[i] == 0:
q.append(i)
while q :
node = q.popleft()
res.append(node)
for nei in graph[node]:
indegree[nei] -= 1
if indegree[nei] == 0:
q.append(nei)
if len(res) == k:
return res
else:
# cycle or not all nodes are connected
return []
r = topology_sort(row_graph,row_indegree)
c = topology_sort(col_graph,col_indegree)
if not r or not c:
return [] # cycle or not all nodes are connected
row_pos = {num : i for i,num in enumerate(r)}
col_pos = {num : j for j,num in enumerate(c)}
for num in range(1,k+1):
matrix[row_pos[num]][col_pos[num]] = num
return matrix

Lessons Learned
이상으로 2392. Build a Matrix With Conditions 문제에 대해 정리해봤습니다. 이 문제를 통해 위상정렬의 개념과 이를 그래프 문제에 적용하는 방법을 배울 수 있었습니다. 사이클이 발생하거나 모든 간선이 제대로 연결되지 않은 경우는 결과 리스트 길이를 판단해서 모든 노드들이 담겨있는지 혹은 추가로 더 담겨있는지 등을 알 수 있었습니다. 특히 위상정렬을 활용하여 주어진 조건을 만족하는 매트릭스를 구성하는 과정에서, 위상정렬의 유일성을 통해 행렬위치가 보장된다는 것을 배웠습니다.
'컴퓨터 공부 > 📚 Leetcode' 카테고리의 다른 글
| [리트코드/leetcode/python] 1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance (0) | 2024.07.26 |
|---|---|
| [리트코드/leetcode/python] 912. Sort an Array (0) | 2024.07.25 |
| [리트코드/leetcode/python] 560. Subarray Sum Equals K (0) | 2024.01.28 |
| [리트코드/leetcode/python] 380. Insert Delete GetRandom O(1) (0) | 2024.01.16 |
| [리트코드/leetcode/python] 1235. Maximum Profit in Job Scheduling (2) | 2024.01.06 |
