



오늘 소개할 문제는 LeetCode 1334번 문제 "Find the City With the Smallest Number of Neighbors at a Threshold Distance"입니다. 이 문제는 그래프 이론과 최단 경로 알고리즘을 이해하는 데 중요한 문제로, 특히 다익스트라 알고리즘을 활용합니다.
문제 설명
리트코드 1334번 Find the City With the Smallest Number of Neighbors at a Threshold Distance 문제에서는 n개의 도시와 도로 정보(edges)가 주어집니다. 각 도로는 두 도시를 연결하며, 그 사이의 거리가 주어집니다. 주어진 distanceThreshold 이하의 거리 내에 있는 이웃 도시의 수가 가장 적은 도시를 찾아야 합니다. 만약 그러한 도시가 여러 개라면, 도시 번호가 가장 큰 도시를 선택합니다. 이 문제는 최단 거리 문제와 관련이 있습니다. 각 도시는 그래프의 노드로, 도로는 그래프의 엣지로 볼 수 있습니다. 문제의 핵심은 각 도시에서 다른 도시까지의 최단 거리를 계산하고, 주어진 거리 임계값 내에 있는 도시의 수를 찾는 것입니다.
문제 해결 과정
1. 초기 접근 : 문제 이해하기
먼저, 각 도시를 노드로, 도로를 엣지로 가지는 그래프로 생각합니다. 각 도시로부터 다른 도시까지의 최단 거리를 구해야 하므로, 최단 경로 알고리즘이 필요합니다. 여기서 다익스트라 알고리즘을 사용하기로 결정했습니다. 다익스트라 알고리즘은 하나의 시작점에서 다른 모든 점까지의 최단 거리를 구하는 데 효율적입니다. 물론, 플로이드 워셜 알고리즘이나 벨만 포드 알고리즘으로 구현하셔도 문제없습니다.
2-1. 다익스트라 알고리즘을 이용한 해결 방법 - 그래프 모델링
그럼 먼저 그래프 모델링을 해봅시다.
주어진 도로 정보(edges)를 바탕으로 그래프를 모델링해야 합니다. 이 때, 인접 리스트를 사용하여 각 도시와 연결된 도로와 거리를 저장합니다. 인접 리스트는 각 노드(도시)에 연결된 이웃 노드와 그 엣지의 가중치(거리)를 저장하는 자료구조 입니다.
graph = [[] for _ in range(n)]
for a, b, cost in edges:
graph[a].append((b, cost))
graph[b].append((a, cost))
위 코드는 n 개의 도시를 나타내는 인접 리스트를 초기화하고, edges 리스트를 통해 도로 정보를 그래프에 추가하는 부분입니다.
2-2. 다익스트라 알고리즘을 이용한 해결 방법 - 최단 거리 계산
이제 해야 할 단계는 최단거리 계산입니다.
각 도시에서 다른 모든 도시까지의 최단 거리를 계산하는 것입니다. 이를 위해 다익스트라, 플로이드, 벨만 포드 등의 알고리즘을 생각할 수 있지만, 저는 여기서 다익스트라 알고리즘을 사용했습니다.
다익스트라 알고리즘의 주요 아이디어는 다음과 같습니다.
1. 시작 노드에서 다른 모든 노드들까지의 거리를 INF(무한대)로 초기화하고, 시작 노드의 거리를 0으로 설정합니다.
2. 우선순위 큐(힙)을 사용하여 현재 가장 짧은 거리에 있는 노드를 선택하고, 그 노드에 갈 수 있는 다른 노드들의 거리를 업데이트 합니다.
3. 이 과정을 큐가 빌 때까지 반복합니다.
INF = int(1e9)
def dijkstra(start):
# 시작 노드에서 각 노드까지의 거리를 무한대로 초기화
distances = [INF] * n
distances[start] = 0 # 시작 노드의 거리는 0으로 설정
q = []
heapq.heappush(q,(0,start)) # (distance, node) 형태로 q 초기화
while q :
current_distance, current_node = heapq.heappop(q)
# 큐에서 꺼낸 노드의 현재 거리가 기록된 거리보다 크면 무시
if current_distance > distances[current_node]:
continue
# 현재 노드와 연결된 모든 이웃 노드(graph[current_node])에 대해 거리 계산
for neighbor, weight in graph[current_node]:
distance = current_distance + weight
# 새로 계산된 거리가 기존 거리보다 작으면 업데이트(더 최단거리로 갈 수 있으니까)
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(q,(distance,neighbor))
return distances # 시작 노드로부터 각 노드까지의 최단 거리 배열 반환
위 함수 dijkstra 는 특정 도시 start 에서 다른 모든 도시에 대한 최단거리를 계산하여 반환합니다.
2-3. 다익스트라 알고리즘을 이용한 해결 방법 - 조건에 맞는 도시 찾기
거의 다 왔습니다. 이제는 조건에 맞는 도시를 찾기만 하면 됩니다.
모든 도시에서 다익스트라 알고리즘을 실행하여 최단 거리를 계산한 후, 각 도시의 distanceThreshold 내에 있는 이웃 도시의 수를 셉니다. 그런 다음, 이 수가 가장 적은 도시를 찾습니다. 만약 동일한 수의 이웃 도시를 가진 도시가 여러 개라면, 도시 번호가 큰 도시를 선택합니다.
min_city = -1
min_count = INF # 최소 이웃 도시 수를 초기화
for i in range(n):
distances = dijkstra(i) # 도시 i를 시작점으로 하는 다익스트라 실행
# 도시 i에서 임계거리 내에 있는 도시의 수 계산
count = 0
for d in distances:
if d <= distanceThreshold:
count += 1
# 조건에 맞는 도시 찾기(같으면, 큰 도시번호가 부여되도록 <= 로 설정)
if count <= min_count:
min_count = count
min_city = i
이 부분에서는 각 도시를 출발점으로 하여 다익스트라 알고리즘을 실행하고, 임계 거리 내에 있는 도시의 수를 계산합니다. 그런 다음, 조건에 따라 가장 적은 수의 이웃 도시를 가진 도시를 찾습니다.
3. 최종 코드 및 결과
import heapq
class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
graph = [[] for _ in range(n)]
for a,b,cost in edges:
graph[a].append((b,cost))
graph[b].append((a,cost))
# print(graph)
INF = int(1e9)
def dijkstra(start):
distances = [INF] * n
distances[start] = 0
q = []
heapq.heappush(q,(0,start)) # (distance, node)
while q :
current_distance, current_node = heapq.heappop(q)
if current_distance > distances[current_node]:
continue
for neighbor, weight in graph[current_node]:
distance = current_distance + weight
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(q,(distance,neighbor))
return distances
min_city = -1
min_count = INF
for i in range(n):
distances = dijkstra(i)
count = 0
for d in distances:
if d <= distanceThreshold:
count += 1
# count = sum(1 for d in distances if d <= distanceThreshold)
if count <= min_count:
min_count = count
min_city = i
return min_city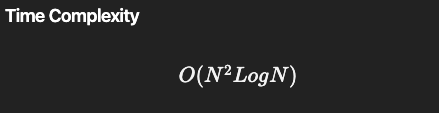
Lessons Learned
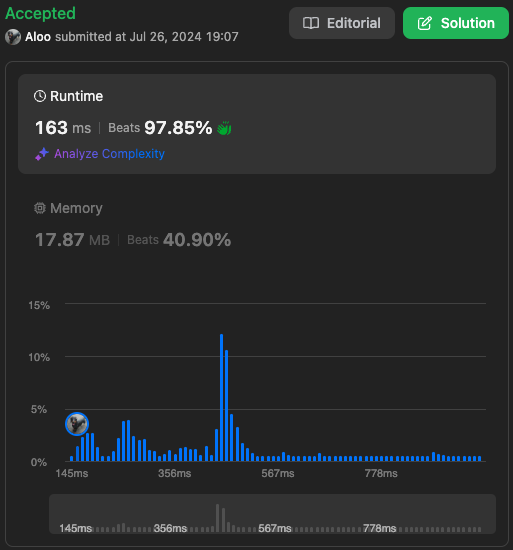
이상으로 1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance 문제에 대해 정리해봤습니다. 이 문제를 통해 다익스트라 알고리즘과 그래프 이론에 대해 학습할 수 있었습니다. 특히, 각 도시 간의 최단 거리를 효율적으로 계산하고, 이를 기반으로 특정 조건을 만족하는 도시를 찾는 과정에서 알고리즘의 중요성을 다시 한번 확인할 수 있었습니다. 그래프 문제를 해결할 때는 주어진 조건과 문제의 특성에 맞는 알고리즘을 선택하는 것이 중요합니다. 이번 문제에서는 다익스트라 알고리즘이 최적의 선택이었습니다.
번외로, 플로이드 워셜 알고리즘으로 푼 코드는 아래와 같습니다.
class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
INF = int(1e9)
dist = [[INF] * n for _ in range(n)]
for i in range(n):
dist[i][i] = 0 # 자기 자신으로의 거리는 0
# 주어진 간선 정보를 기반으로 거리 초기화
for a,b,cost in edges:
dist[a][b] = cost
dist[b][a] = cost
for k in range(n):
for i in range(n):
for j in range(n):
dist[i][j] = min(dist[i][k] + dist[k][j],dist[i][j])
min_city = -1
min_count = INF
for i in range(n):
count = 0
for j in range(n):
if dist[i][j] <= distanceThreshold:
count += 1
if count <= min_count:
min_count = count
min_city = i
return min_city
이 문제에서 플로이드-워셜의 시간복잡도는 O(N^3)으로 다익스트라 알고리즘보다는 비효율적이었습니다.

'컴퓨터 공부 > 📚 Leetcode' 카테고리의 다른 글
| [리트코드/leetcode/python] 40. Combination Sum II (0) | 2024.08.14 |
|---|---|
| [리트코드/leetcode/python] 912. Sort an Array (0) | 2024.07.25 |
| [리트코드/leetcode/python] 2392. Build a Matrix With Conditions (0) | 2024.07.21 |
| [리트코드/leetcode/python] 560. Subarray Sum Equals K (0) | 2024.01.28 |
| [리트코드/leetcode/python] 380. Insert Delete GetRandom O(1) (0) | 2024.01.16 |
