코딩 테스트에서는 제약사항에 따라 빠르게 풀리는 알고리즘으로 문제를 풀어야 할 때가 있습니다. 시간 복잡도를 기준으로 알고리즘을 택해야 하는데, 그럼 시간 복잡도라는 것이 도대체 무엇일까요?
📖 시간 복잡도란?
알고리즘의 성능을 나타내는 지표로, 입력 크기에 대한 연산 횟수의 상한을 의미합니다. 시간 복잡도는 낮으면 낮을 수록 좋습니다.
예를 들어, 1차원 배열에서 특정 값을 찾는다고 가정해봅시다.
어떤 경우에 가장 빨리 값을 찾게 되고, 어떤 경우에 가장 늦게 값을 찾게 될까요?
1) 값을 가장 빨리 찾는 경우
- 값을 가장 빨리 찾는 경우는 검색 시작 위치에 찾고자 하는 값이 바로 있는 경우입니다.
target = 1
array = [1,5,2,6,3,17,13,9]
# 찾고자 하는 값 1이 array 배열의 가장 첫 번째 자리에 위치해 있어 바로 찾을 수 있습니다.
2) 값을 가장 늦게 찾는 경우
- 값을 가장 늦게 찾는 경우는 아예 찾으려는 값이 배열 내에 없거나, 배열의 가장 마지막 위치에 값이 있는 경우입니다.
target = 100
array = [1,5,2,6,3,17,13,9]
# 찾고자 하는 값 100 이 array 배열 어디에도 없습니다.
# 이 경우 비교 횟수는 8번입니다. (target과 array의 각 원소를 차례대로 비교하면서 찾아가기 때문입니다.)
📖 알고리즘 수행 시간을 측정하는 방법?
알고리즘 수행 시간을 측정하는 방법으로는 절대 시간을 측정하는 방법과 시간 복잡도를 측정하는 방법이 있습니다.
1) 절대 시간을 측정하는 방법
■ 절대 시간을 측정하는 방법은 말 그대로 시간을 측정하면 됩니다. 프로그램을 실행하여 결과가 나올 때 까지의 시간을 측정하면 되지만, 이 방법은 프로그램을 실행하는 환경에 따라 달라질 수 있기에 코딩테스트에서는 잘 활용하지 않습니다.
2) 시간 복잡도를 측정하는 방법
■ 시간 복잡도를 측정하는 방법은 앞서 검색 문제에서 살짝 언급한 '연산 횟수'와 관련이 있습니다. 즉, 시간 복잡도는 알고리즘이 시작한 순간부터 결과값이 나올 때까지의 연산 횟수를 나타냅니다.
■ 보통 시간 복잡도는 "최선(best)→보통(normal)→최악(worst)"의 경우로 나눕니다.
■ 앞의 검색 예제에서는 최선의 연산 횟수가 1번, 최악의 연산 횟수가 8번이 된 셈입니다.
■ 그러나 이렇게 최선은 1, 최악은 8번이라는 특정한 입력 크기에 따른 연산 횟수로 시간 복잡도를 이야기 하는 것은 특정 상황에 한한 것이므로 무의미합니다. 아까 검색 예제에서 array의 길이가 1 이면, 최선,보통,최악의 경우 모두 연산횟수가 1 이 됩니다.
■ 다시 말해, 시간 복잡도는 특정 입력 크기에 한하여 연산횟수를 기준으로 측정하면 안 됩니다. 대신에, 입력 크기를 N 이라고 일반화
하여 연산 횟수의 추이를 나타내야 하죠. 이런 방식으로 시간 복잡도를 표현하는 방법을 바로 점근적 표기법(빅오 표기법) 이라 합니다.
📖 최악의 경우 시간 복잡도를 표현하는 빅오 표기법
가장 많이 사용하는 접근적 표기법은 상한선을 활용하는 방법입니다. 이 표기법을 빅오 표기법(big O notation) 이라고 하는 것입니다.
빅오 표기법은 어떤 프로그램의 연산 횟수가 f(x) 라고 할 때, 함수의 최고차항을 남기고 차수를 지워 O(...) 와 같이 표기합니다. 예를 들어,
어떤 프로그램의 연산 횟수 f(x) = 5x^2 + 6x + 7 라면, 시간복잡도는 O(x^2) 로 표현할 수 있겠죠.
그럼 예시를 더 살펴보면서, 이해를 강화해봅시다.
| 수식 | 빅오 표기 | 설명 |
| 3x^2 + 6x + 8 | O(x^2) | 최고차항 x^2만 남습니다. |
| x + logx | O(x) | 다항함수와 로그함수로 구성되어 있는데, 증가폭이 더 낮은 로그함수는 사라지고 다항함수를 기준으로 x 만 남습니다. |
| 2^x + 10x^5 + 8x^3 | O(2^x) | 지수함수는 다항함수보다 빠르게 증가하므로, 지수함수를 기준으로 2^x 만 남습니다. |
그럼 왜이렇게 표기를 할까?
다음과 같은 코드가 있다고 해보자.
def solution(n):
count = 0
# 반복문 1 : n^2 번 연산 수행
for i in range(n):
for j in range(n):
count += 1
# 반복문 2 : n 번 연산 수행
for k in range(n):
count += 1
# 반복문 3 : 3n 번 연산 수행
for i in range(2*n):
count += 1
# 반복문 4 : 5번 연산 수행
for i in range(5):
count += 1
print(count) # 59 -> (n이 6일 때, 6^2 + 6 + 2*6 + 5 = 59)
solution(6) # 함수 호출
solution(6) 을 호출하면, 6^2 + 3* 6 + 5, 즉 연산횟수는 59 가 됩니다. 이 때, solution() 함수는 식으로 표현하면 다음과 같이 표현할 수 있습니다.
f(x) = x^2 + 3x + 5
이 때, 다음을 만족하는 C 가 있으면 f(x)의 최악의 시간 복잡도는 O(g(x)) 라고 쓰는 것입니다.
- 특정 x 시점 이후부터 항상 f(x) <= C * g(x) 를 만족
- C 는 상수
g(x)에 상수 C를 곱했을 때, 특정 시점부터 f(x) 를 넘어서는지 여부를 보면 되는 것이죠. 위 f(x)를 예시로 하면, 적절한 C와 g(x)를 찾으면 아래와 같습니다.
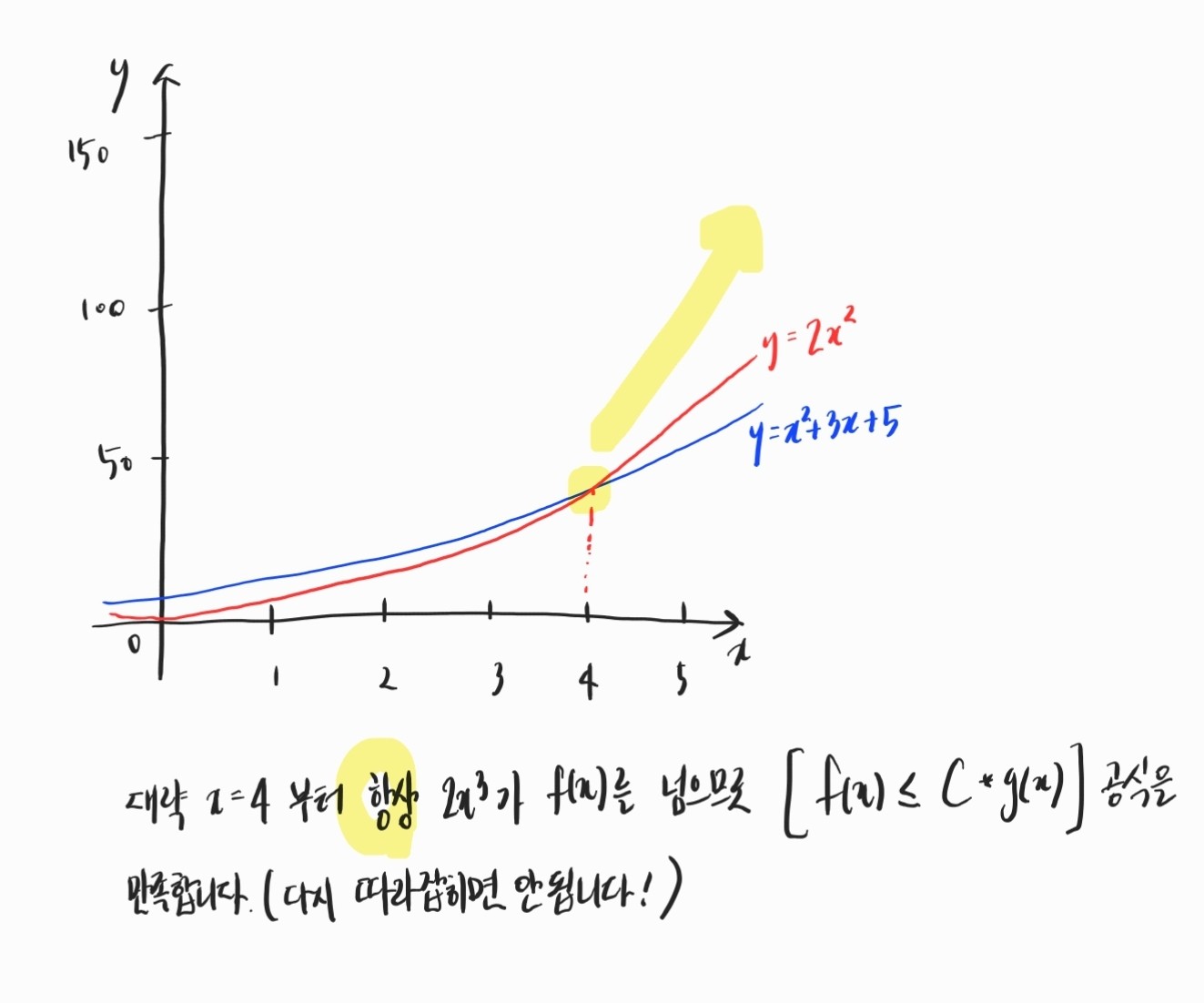
따라서, f(x) 의 시간 복잡도는 g(x)가 x^2 이기 때문에, O(x^2) 라고 할 수 있습니다.
※ 추가문제 입니다.
| 수식 | 빅오 표기 | 설명 |
| 3x^2 + 5x + 6 | O(x^2) | 최고차항 x^2만 남습니다. |
| x + logx | O(x) | 다항함수와 로그함수로 구성되어 있는데, 증가폭이 더 낮은 로그함수는 사라지고 다항함수를 기준으로 x 만 남습니다. |
| 2^x + 10x^5 + 5x^2 | O(2^x) | 지수함수는 다항함수보다 빠르게 증가하므로, 지수함수를 기준으로 2^x 만 남습니다. |
각 수식들을 f(x) 라 할 때, 위 수식을 만족하는 C*g(x) 를 찾아보고 그래프도 그려봅시다.
1) 3x^2 + 5x + 6
: 함수 f(x) = 3x^2 + 5x + 6 와 "f(x) <= C * g(x)" 를 만족하는 C * g(x) = x^3 을 찾을 수 있습니다.
: f(x) 는 2차 다항식이고 g(x) = x^3 으로 3차 다항식이기 때문에 g(x)가 f(x) 보다 더 빠르게 증가합니다.
같은 평면에 그려보면, 아래와 같습니다.

하지만, 우리는 시간복잡도를 고려하여 g(x) 를 선택할 때, 우리는 가장 가능한 낮은 시간복잡도를 가진 g(x)를 찾아야 합니다.
(x)의 시간복잡도는 실질적으로 O(x^2)에 가까우니, 이를 상회하는 가장 낮은 시간복잡도도 역시 O(x^2) 일 것입니다.
함수 f(x) = 3x^2 + 5x + 6 와 이를 상회하는 C * g(x) = 4x^2 (여기서 C=2)를 찾을 수 있고 이를 같은 평면에 그리면 아래와 같습니다.
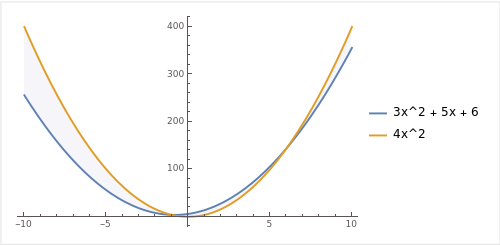
이 그래프를 통해 C * g(x) = 4x^2 가 f(x) = 3x^2 + 5x + 6 보다 항상 큰 것을 확인할 수 있습니다. x가 증가할수록 그 차이는 더 커집니다.
따라서 시간복잡도는 O(x^2) 가 됩니다.
2) x + logx
: 함수 f(x) = x + logx 와 이를 상회하는 g(x)함수로 g(x) = x^2를 선택할 수 있습니다.
: f(x)는 선형 함수와 로그 함수의 합이고 g(x) = x^2 으로 2차 다항식이기 때문에 x가 증가함에 따라 x^2는 x + logx 보다 더 빠르게 증가하므로, 적절한 상수 C를 찾으면 f(x) <= C * g(x) 를 만족할 수 있습니다.

하지만, 역시 마찬가지로, 시간복잡도를 고려하여 g(x) 를 선택할 때, 우리는 가장 가능한 낮은 시간복잡도를 가진 g(x)를 찾아야 합니다.
x가 증가함에 따라 log(x)는 x보다 훨씬 느리게 증가합니다. 따라서, f(x)의 시간복잡도는 실질적으로 O(x)에 가깝습니다.
이를 고려할 때, 우리는 g(x) = 2x 를 선택하는 것이 가장 최적의 시간복잡도를 가진 선택일 수 있습니다. 이 때, C를 다른 적절히 큰 값으로 설정해서 f(x) <= C * g(x) 를 만족하게 할 수 있습니다.
같은 평면에 그려보면, 아래와 같습니다.

이 그래프를 통해 C * g(x) = 2x 가 f(x) = x + logx 보다 항상 큰 것을 확인할 수 있습니다. x가 증가함에 따라 이 차이는 더 커집니다.
따라서, 따라서 시간복잡도는 O(x) 가 됩니다.
3) 2^x + 10x^5 + 5x^2
: 함수 f(x) = 2^x + 10x^5 + 5x^2 와 "f(x) <= C * g(x)" 를 만족하는 C * g(x) = 11x^5 을 찾을 수 있습니다.
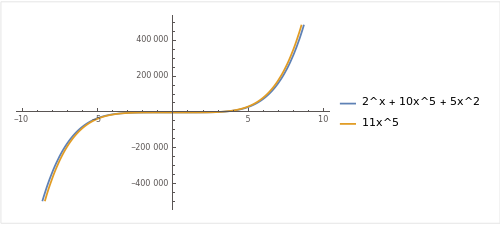
하지만, 결국 f(x)는 지수함수이고, g(x)는 다항함수이기 때문에, f(x)가 g(x)보다 훨씬 빠르게 증가합니다.
즉, 지수함수의 성장률은 다항함수의 성장률을 결국 초과하게 되는 것입니다.
따라서, 어떤 상수 C와 다항함수 g(x)를 사용하여도, f(x) <= C * g(x) 를 영원히 만족시키는 것은 불가능합니다.
같은 평면에 그려보면, 아래와 같습니다.
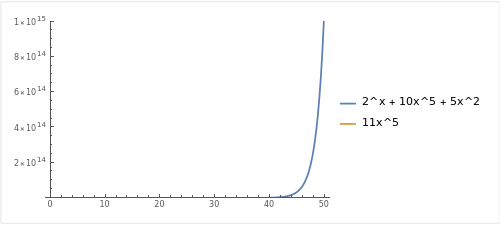
지수함수의 성장률은 다항함수보다 항상 더 빠르기 때문에, x가 충분히 큰 값으로 갈 수록 2^x 는 어떤 다항함수보다도 더 큰 값을 가지게 됩니다. 이러한 이유로 f((x) 를 상회하는 C*g(x) 를 찾는 것은 불가능한 문제입니다.
따라서, 따라서 시간복잡도는 f(x)의 시간복잡돈인 O(2^x) 가 됩니다.
3) 2^x + 10x^5 + 5x^2 과 같은 이유로 빅오 표기법에서는 최고차항만 남기고 차수를 지우는 것입니다.
로그함수는 다항함수보다 느리게 증가하고, 지수함수는 다항함수보다 빠르게 증가합니다. 그 성장률을 생각해보면, x 값이 무한이 커지게 될 때, 그 격차는 더 심해지는 것입니다.

📖 시간복잡도를 코딩테스트에 활용하는 방법은?
이제 시간복잡도를 표현하는 방법이 빅오 표기법이라는 것을 알았습니다. 그럼 코딩 테스트에서는 어떻게 이런 시간복잡도를 활용할 수 있을까요?
코딩테스트 문제에는 제한시간이 있으므로 문제를 분석한 후, 빅오 표기법을 활용해서 해당 알고리즘을 적용했을 때 제한 시간 내에 출력값이 나올 수 있을지 확인해볼 수 있습니다.
보통은 다음 기준으로 알고리즘을 선택합니다.
컴퓨터가 초당 연산할 수 있는 최대 횟수는 1억 번이다.
코딩테스트의 문제는 출제자가 의도한 로직을 구현했다면, 대부분의 코드는 정답처리 되도록 설계되어 있습니다.
따라서, 연산 횟수는 1000~3000만 정도(10^8 직전까지) 로 고려해서 시간복잡도를 생각하면 됩니다.
예를 들어, 제한시간이 1초인 문제는 연산 횟수가 3000만(10^8) 이 넘는 알고리즘을 사용하면 안됩니다.
| 시간복잡도 | 최대 연산 횟수 |
| O(N!) | 10 |
| O(2^n) | 20~25 |
| O(N^3) | 200~300 |
| O(N^2) | 3000~5000(10^3) |
| O(NlogN) | 100 만(10^6) |
| O(N) | 1000~2000 만 (10^8) |
| O(logN) | 10억 (10^9) |
아까 맨 처음 예시로 돌아가서 본다면, 이렇게 하나하나 배열의 각 원소를 확인하는 방식은 시간복잡도가 O(N) 입니다.
(여기서 N 은 배열의 길이겠지요)
taegt = 33
array = [1,5,2,6,3,17,13,9]
보통 O(N)이 허용하는 연산 횟수는 1000 만이므로, 데이터의 개수가 1000 만개 이하이면, 이 알고리즘은 사용해도 됩니다.
하지만, 데이터의 개수가 1억개다, 예를 들어 배열의 길이가 1억이다. 그러면, O(N) 으로는 풀면 시간초과가 날 수 있습니다.
이렇듯, 문제에 따라 시간복잡도를 고려해야 합니다.
📖 시간복잡도 계산해보기
문제 1) 별 찍기 문제
: 숫자 N을 입력받으면 N번째 줄까지 별을 1개부터 N개까지 늘려가며 출력하라는 것입니다.
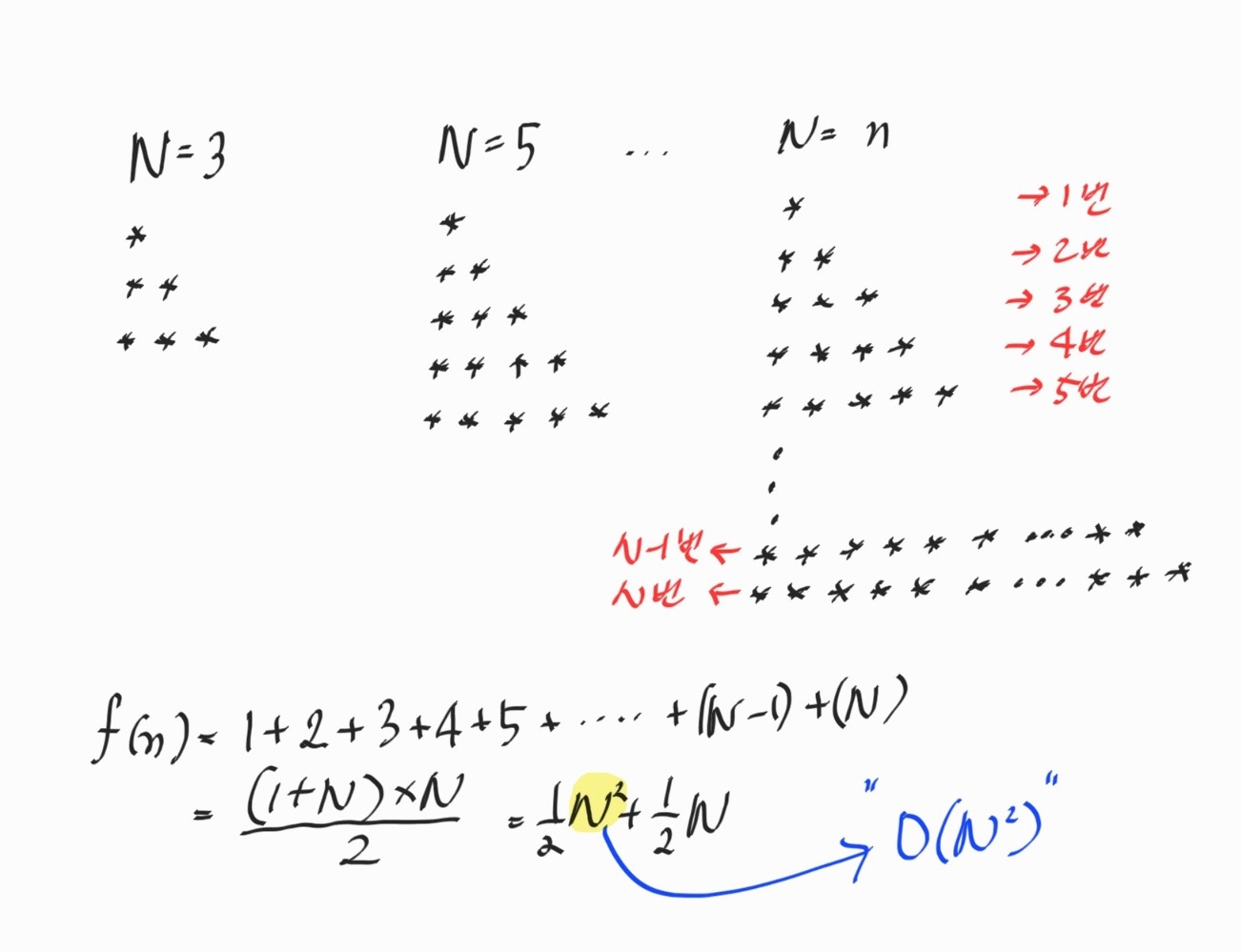
N까지 별을 찍는 문제에서의 연산횟수는 1번 계산, 2번 계산,..., N-1 번 계산, N번 계산 으로 계산이 됩니다.
결국, 최종 연산 횟수 f(N)은 위와 같고, 빅오 표기법으로는 O(N^2) 이라고 할 수 있습니다.
문제 2) 박테리아 수명 문제
: 초기 박테리아 세포 개수가 N일 때, 해마다 세포 개수가 이전 세포 개수의 반으로 준다면, 언제 모든 박테리아가 죽을지 계산해야 합니다.
예를 들어, N 이 32인 경우, 모든 박테리아는 6년이면 소멸합니다.
32 → 16 (1년) → 8(2년) → 4(3년) → 2(4년) → 1(5년) → 0(6년)
Y 년 후의 박테리아 수는 (1/2)^Y * N 이고 이 박테리아가 최초로 1 보다 작아질 때를 수식으로 나타내면, 다음과 같습니다.
(1/2)^Y * N <=1
→ N <= (2)^Y
→ log(2)N <= Y
즉, 이 알고리즘은 O(logN)의 시간복잡도를 가진다는 것을 알 수 있습니다.
💡앞으로 문제를 풀 때, 특정값을 계속 반으로 줄이는 동작을 한다면 시간복잡도는 O(logN) 이라고 생각하면 됩니다. 시간복잡도가 O(logN)인 문제들은 이후 정렬이나 이진 트리를 공부하면서 다시 살펴보겠습니다.
💡상한선은 빅-오 표기법, 하한선은 빅-오메가 표기법으로 표시합니다.
💡입력 크기에 따른 연산 횟수의 추이를 활용해서 시간 복잡도를 표현하는 방법을 점근적 표기법이라고 한다.
💡시간 복잡도를 빅오 표기법으로 나타내려면, 데이터 개수 N에 대해 연산 횟수를 일반화 한 후 최고차항을 남기고 차수를 제거하면 된다.
'컴퓨터 공부 > 🧮 알고리즘' 카테고리의 다른 글
| [코테] 코딩 테스트 합격자 되기 2주차 - 배열 (0) | 2024.01.12 |
|---|---|
| [코테] 코딩 테스트 합격자 되기 1주차 - 코딩 테스트 필수 문법 (4) | 2024.01.07 |
| 이진 탐색 - 탐색 범위를 반으로 좁혀가며 탐색하는 알고리즘 (0) | 2021.08.29 |
| 그래프 알고리즘 2 - 코딩 테스트에서 자주 등장하는 기타 그래프 이론 (0) | 2021.08.25 |
| 그래프 알고리즘 1 - 코딩 테스트에서 자주 등장하는 기타 그래프 이론 (0) | 2021.08.25 |
