[백준/알고리즘/python/java] 2004번 - 조합 0의 개수

이미지를 누르면 문제링크를 보실 수 있습니다.

[2004 - 조합 0의 개수]

일단, 문제 설명이 매우 짧다는 것은 어렵다는 소리일지도 모른다.

흔히 우리가 생각하는 방식으로 풀면 시간초과가 날 가능성이 높기 때문이다.

특히, 이 문제는 n,m 의 범위가 20억까지 들어올 수 있다는 설명을 보고 뭔가 다른 방식으로

풀어야 겠다는 생각이 들었다.

 

'팩토리얼 0 의 개수' 문제처럼 끝자리 0의 개수를 출력하는 것은 맞지만,

이번에는 이항계수 개념이 도입된 문제였다. 

이항계수(Binomial Coefficient)는 조합론에서 등장하는 개념으로 주어진 크기 집합에서

원하는 개수만큼 순서없이 뽑는 조합의 가짓수를 일컫는다.

2를 상징하는 '이항'이라는 말이 붙은 이유는 하나의 아이템에 대해서는 '뽑거나' , '안 뽑거나' 두 가지의 선택만이 있기 때문이다. (출처 : shoark7.github.io/programming/algorithm/3-ways-to-get-binomial-coefficients)

 

nCm 의 계산공식은 다음과 같다.

m을 r로 대체

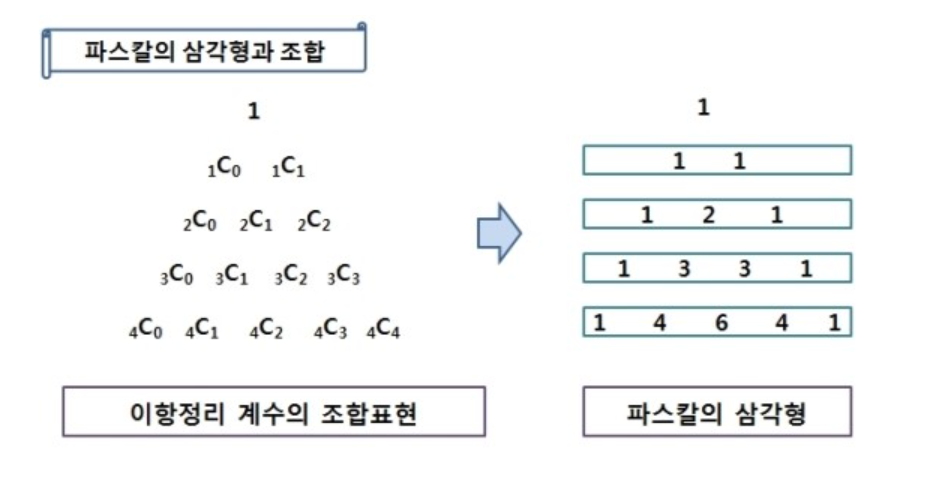
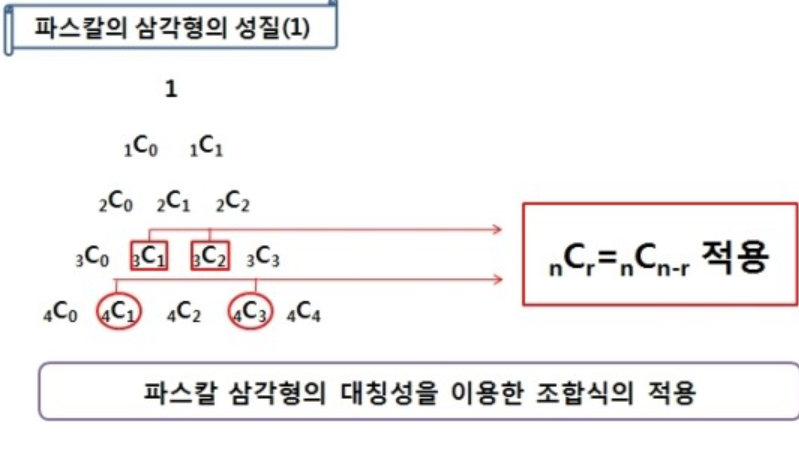
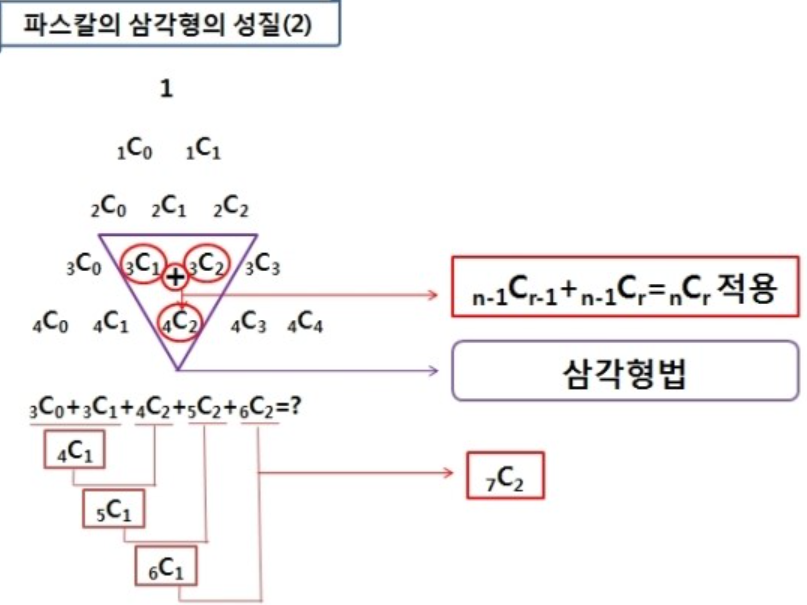
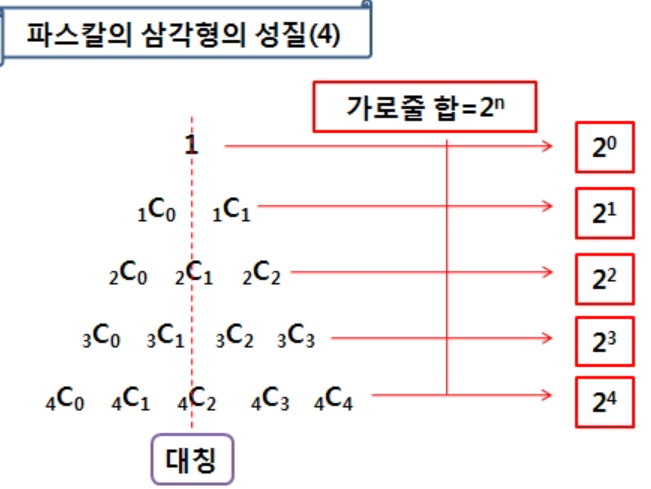
이항정리는 파스칼 삼각형과 연관이 깊다.

이항정리한 계수 값들이 파스칼의 삼각형으로 표현되기 때문이다.

파스칼 삼각형의 성질은 메모이제이션(동적계획법)에서도 쓰이는 알고리즘이기 때문에 알아두면 유용하다.

(고등학교 때 배운 파스칼 삼각형의 성질을 잠깐 복습해보자)

 

  파스칼의 삼각형의 값들을 이항계수의 조합표현으로 연결해서 표현하면 위와 같은 모양으로 다시 표현할 수 있다.

 

위의 조합 식을 바탕으로 그 전에 배운 조합식을 적용하면, 파스칼의 삼각형의 대팅성에 의해 좌우의 같은 위치의 값들과 같게 됨을 확인할 수 있다.

 

위의 두 개의 값을 더하면 아래의 값이 된다. 이를 삼각형 법이라고도 한다.

왼쪽의 모든 라인과 오른쪽의 모든 라인이 1이라는 값을 가진다는 점을 이용하여 응용한 것이다. 이를 하키스틱의 법칙이라고도 한다. 자주 쓰이는 공식이니 기억해두자.

파스칼의 삼각형은 가로줄의 수들을 모두 합하면 2의 거듭제곱으로 표현됨을 알 수 있다.

 

나는 팩토리얼로 계속해서 곱하면서 조합(Combination)을 구하면 분명 시간초과가 날 것 같아서

처음에 동적계획법으로 푸는 문제인 줄 알았다.

우선, (동적계획법을 이용한 조합 계산)은 코드로 남겨보겠다.

 

import sys
max_NUM = sys.maxsize   # 혹시나 max_NUM 을 선언해봐서 범위에 넣어봤지만 안됐다.


def combi(n, m):        # 메모이제이션 기법을 활용한 조합 계산 함수
    for i in range(n+1):
        for j in range(min(i, m)+1):
            if (j == 0 or j == i):
                memoi[i][j] = 1
            else:
                memoi[i][j] = memoi[i-1][j-1] + memoi[i-1][j]
    return memoi[n][m]


n, m = map(int, input().split())
memoi = [[0 for col in range(1000)] for row in range(1000)]  # 이 부분에서 배열 크기를 20억까지 못 만든다.
print(combi(n, m))

 

그런데, 메모이제이션 기법을 사용하려면, 우선 배열을 선언해야 할 터인데,

20억까지의 수(2,000,000,000)를 저장하기에는 부담이 될 수 있었다.

파이썬 배열 최대 크기에 대해 관련 내용을 찾아보니,

 

▶ 999,999,999 하면 메모리에러 ◀

    천만부터 느려지고

    2억까지 가능

    3억부터 메모리에러

    백만까지 스무스하게 빠르게 생성 가능 

▶ 100,000,000 (일억)이 381 MB 크기 ◀

라고 한다.

20억 까지 입력 가능하니까 당연히 메모이제이션 방식으로 푸는 법은 아니란 소리였다.(메모리 에러)

 

 

따라서, 다른 식을 생각해내는데 어떠한 수에 0이 생기는 경우는 10이 만들어지는 경우라고 했다.

( 팩토리얼 0의 개수 문제에서도 살펴보았다.)

그렇다면 10은 언제 만들어질까? 역시 10은 2와 5의 곱으로 만들어지는 것도 알고있다.

 

그렇다면, 우리는 주어진 수에서 0의 개수를 구하려면

2가 몇번 나누어지는지와 5가 몇번 나누어지는지를 구하고 2 와 5의 개수중 더 작은 개수를 선택하면 된다.

(m과 n을 입력받았을때 m! 을 m! 과 (m-m)! 로 나눈 값이 조합이기 때문이다.)
즉,

0의개수 =

m!가 가지고 있는 2의 개수 - n!이 가지고 있는 2의 개수 - (m-n)!이 가지고 있는 2의 개수

or

m!가 가지고 있는 5의 개수 - n!이 가지고 있는 5의 개수 - (m-n)!이 가지고 있는 5의 개수

중에 작은 수

(최종 소스 코드는 아래와 같다.-python)

def cnt2(n):  # 2가 몇번 나누어지는지를 구한다.
    n2 = 0
    while(n != 0):
        n //= 2
        n2 += n
    return n2


def cnt5(n):  # 5가 몇번 나누어지는지를 구한다.
    n5 = 0
    while(n != 0):
        n //= 5
        n5 += n
    return n5


n, m = map(int, input().split())
print(min(cnt2(n)-cnt2(m)-cnt2(n-m), cnt5(n)-cnt5(m)-cnt5(n-m)))

조합 계산기 사이트 링크 : ko.numberempire.com/combinatorialcalculator.php

 

솔직히, 쉽게 이러한 규칙들을 찾아내기 번거로울 수 있다.생각을 깊게 해보고 써보면서 규칙을 발견하는 것도 결국 실력이다. 많이 발전해야겠다.